F1: Power and Downforce

With Formula 1 coming to Austin later this year I figured I should probably learn something about the "sport."^[1] The most interesting thing about F1 is less about the petty politics and more about the way that the teams modify cars from track to track.

In 2021 the F1 season consists of 23 races which take place everywhere from Azerbaijan to Japan. However, each track is unique both in terms of its structure and location which leads the teams to make various tradeoffs between downforce and power.

Downforce is downward lift which basically pushes the car into the ground the faster the car goes.^[2] As a rough heuristic, you want power where the track is very straight and you want downforce when the track has lots of turns.

High Power

The Autodromo Nazionale Monza (Monza) in Italy is a classic "power track"^[3] since it is relatively straight. As you might expect, the Monza track is home to the fastest lap time ever recorded.

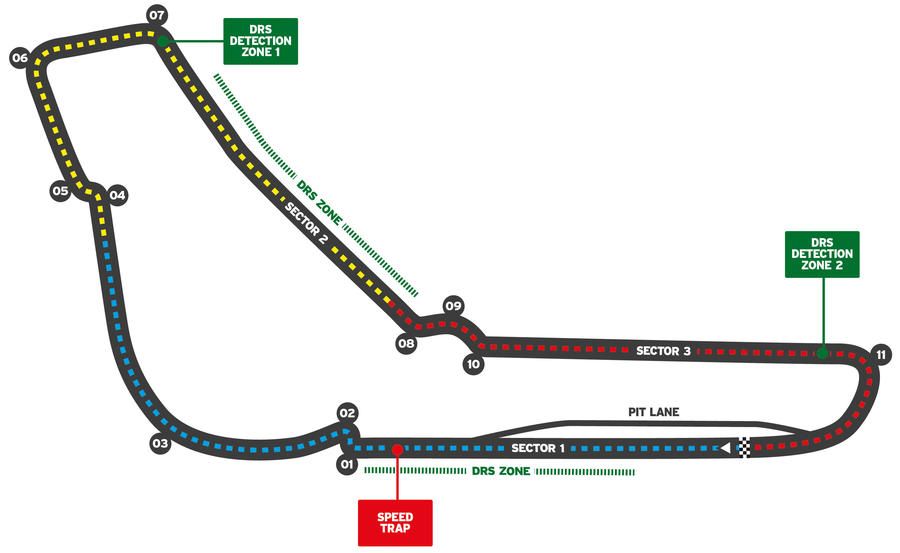
High Downforce

On the other hand, the Suzuka Circuit in Japan is one that would be a classic "downforce track" since it contains many intricate turns.

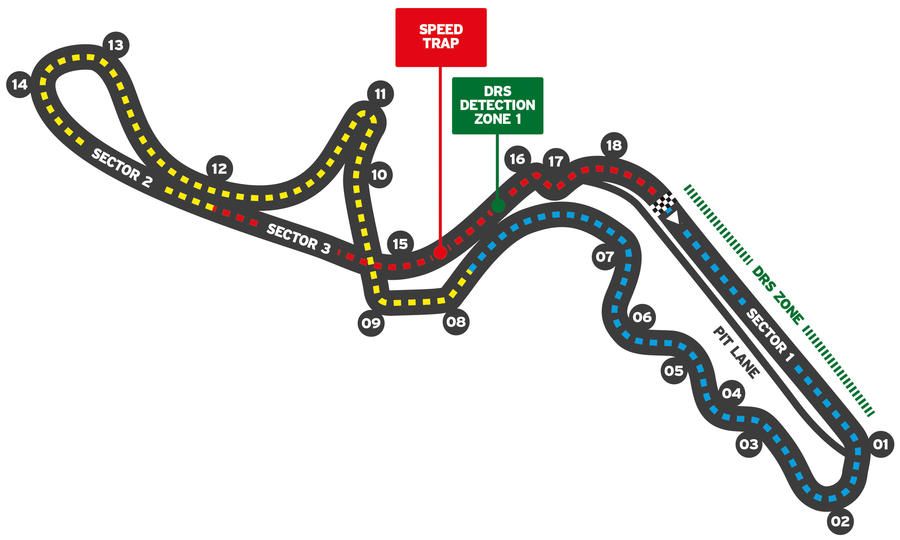
How Do Power and Downforce Relate?

Now that we've established tracks that are high "power" and high "downforce" we are in a better position to understand the way these two forces interact.

First, we know that power is a vector function of both force and velocity which can be expressed as follows:

\[P = F \times V\]

Second, we know that drag is a function of the density of fluid it is traveling through, the speed of the object relative to the fluid, the drag coefficient, and the cross sectional area

\[F_D = \frac{1}{2}\rho \times v^2 \times C_D \times A \]

For reference:

• ( F_D ) is drag
• ( rho ) is the density of fluid which in most races is going to be the air density which is a function of altitude, time of day, weather and a bunch of other exogenous factors
• $v^2$ is the speed of the object relative to the fluid
• $C_D$ is the drag coefficient
• $A$ is the cross sectional area

We can combine the two equations^[4] which gives us:

\[ P = \frac{1}{2}\rho \times C_D \times A \times v^3 \]

In a race you can't really change the $\rho$ since that's tantamount to changing the elevation of the track. However you can reduce the size of the wing hitting the air ($A$) and you can also try to reduce the drag coefficient.

Minimizing $C_D$ and $A$ which means making the wing smaller and more aerodynamic which, all elese equal, means you need less force to achieve a specific velocity. This highly simplified and styalized version is what every F1 team is analyzing at each and every track.

High Power?

Let's look at one last example: the Autódromo Hermanos Rodríguez Grand Prix Circuit in Mexico City.

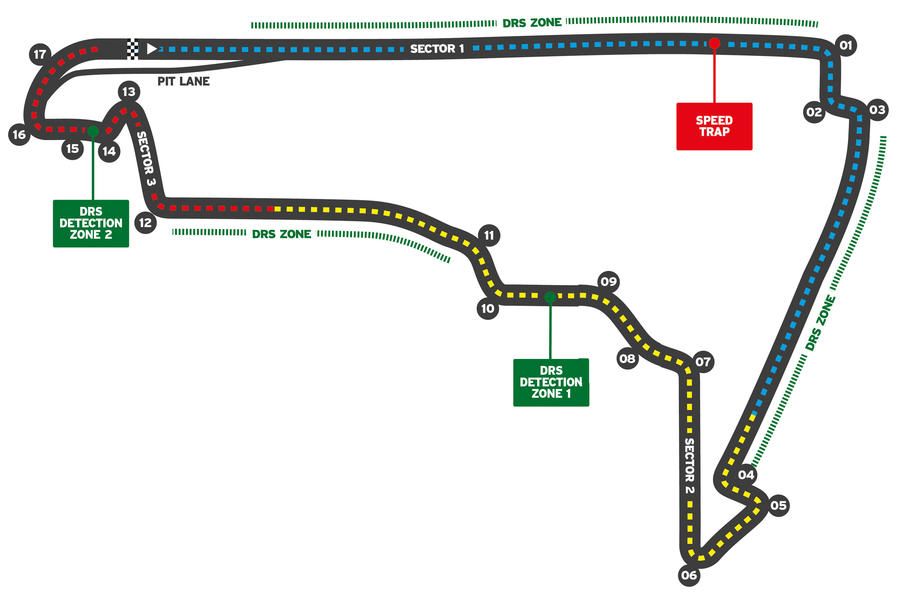
Looking at the track it seems like there are a lot of straights so you may be tempted to think that it's a track that biases to power. However, this is where that pesky $\rho$ comes into play. Recall, $\rho$ stands for the density of fluid or the air density. Turns out Mexico City is ~7,350ft above sea level and air density decreases as you go higher.

If we increase $\rho$ and hold everything else constant, we can see that the car will be generating less downforce at a given speed which actually means that teams may be better off with a more aggressive wing regime than they would otherwise use with such a straight track.