How to Share a Secret
Review of "How to Share a Secret", Adi Shamir's famous paper which asks "How do you divide data D into n pieces in such a way that D is easily reconstructable from any k pieces, but even complete knowledge of k - 1 pieces reveals absolutely no information about D."
In 1979, Adi Shamir, a renowned cryptographer, Turing Award recipient and co-inventor of the Rivest-Shamir-Adleman (RSA) algorithm, wrote a seminal paper about how to share cryptographic keys titled "How to Share a Secret".
The paper is an attempt to address the following question:
[How do you] divide data D into n pieces in such a way that D is easily reconstructable from any k pieces, but even complete knowledge of k - 1 pieces reveals absolutely no information about D.
He starts with a combinatorial problem:

How does he get this minimal solution? Observe that if we have a cabinet with 11 locks and we need 6 of them in order to actually open the cabinet we need to choose 6 of the 11.

Thus for the locks we can express this as follows: $$11 \choose 6$$ which can be simplified as follows: $$= \frac{11!}{6! \times 5!} = 462$$
For the number of keys, we are going to invert the problem. If you have a group of 5 scientists this means they cannot open a lock. If you have an individual A, adding A to the group of 5 means that now you should be able to open the lock. In other words, starting with the individual A you now have a pool of 10 scientists left and from that pool of 10 you need to choose 5 of them.
Thus, for the number of keys we can express this as: $$10 \choose 5$$ which can be simplified as follows: $$= \frac{10!}{5! \times 5!} = 252$$.
Can you imagine you are working on the Manhattan Project and running around Los Alamos with \(252\) keys? There's no way. More importantly, factorial solutions are the least performant algorithms. So, like any good algorithm designer, Shamir asks "can we do better?" by "generalizing the problem to one in which the secret is some data \( D \) into \(n\) pieces such that

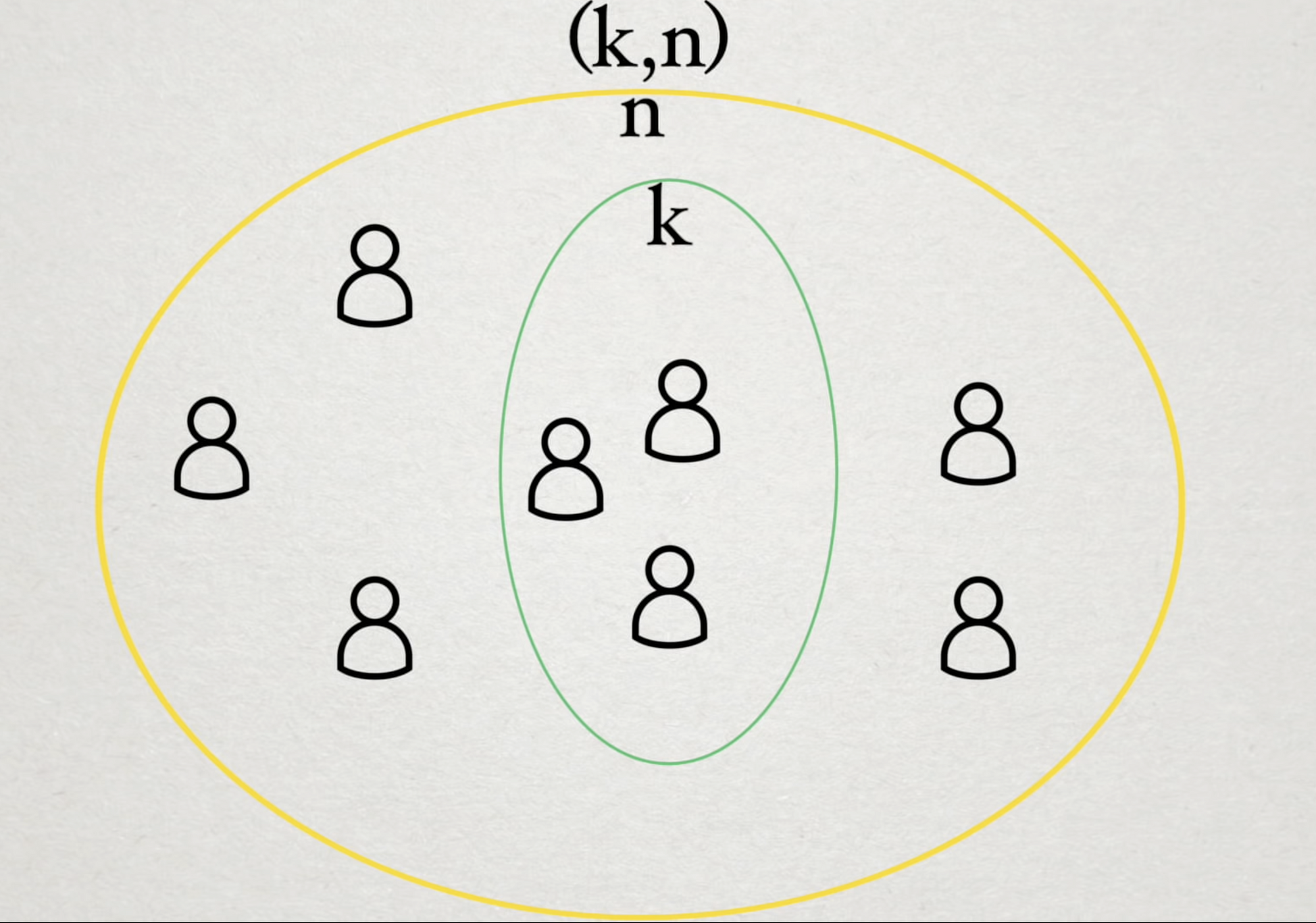
Why not just keep the key in one secure location instead of splitting it into pieces? In fact, what's the use case around splitting? Shamir points out that a single location is the most secure but is also the most unreliable method of storing these keys. You could take the entire key and put it in multiple places, but if one of those locations is compromised, the key is completely compromised. The \( (k, n)\) scheme being proposed here lets you lose \( k-1 \) of the \( n \) pieces and still not reveal the entire key.

Shamir goes on to enumerate the use case of this type of threshold scheme relative to RSA (which he helped invent) by talking about the tradeoffs between secrecy/reliability and safety/convenience. If a company has a secret key and you give the secret key to each of the executives you have a system that is convenient but easy to misuse since you are exposed if one of the executives defects. If the company requires 3 signatures in order for any transaction to go through you have a safe but inconvenient system.

Finally, Shamir walks through the threshold scheme which is predicated on Claude Shannon's idea of perfect secrecy which holds that a ciphertext maintains perfect secrecy if the attacker's knowledge of the contents of the message is the same both before and after the adversary inspects the ciphertext. In short, every key needs to look the equally likely as every other key.
In order to generate this equiprobable distribution, we need to introduce randomness. The IEEE Information Theory Society has a phenomenal example in their video on secret sharing. Let's say you have an image that you want to keep secret. This image is simply a bunch of bits and if you add random bits to the original image you are going to get a random image.

If an attacker were to see the output, that would not leak any information about the original image that we want to keep secret. To get the original image, we would essentially need to subtract the new image from the old image.

This same principle holds true with numbers. We can take a number that we want to keep secret (like, say, a bank account) and add a random number to that which yields a seemingly random number.

To figure out the original number we want to keep secret we would need to bring the two entities with the random number and the random secret together and would need to do a similar operation.

However, you'll notice that in these examples, all the shares are needed to generate the secret. Shamir notes that this type of system will not scale both because of the factorial number of keys you'd need to share and also from a usability standpoint since you'd need everyone in the system to cooperate or else the secret is going to be lost. This kind of single point of failure is a problem and is what Shamir's algorithm is meant to solve so you only need a subset of the people with keys.

Let's recall what we are trying to solve. We are looking for a way to take some data \( D \) and split it into \( k \) pieces in such a way that even if an attacker knows \( k-1 \) pieces, we still won't leak any information about \( D \). Shamir's algorithm essentially solves this problem by suggesting that the secret is a point in space (and if the secret is not a number, he assumes we can figure out a way to make it a number).

Recall that the formula for a line is \( y = mx + b \). If we have \( 3 \) people and we only want \( 2 \) to be needed to recover the secret we can plot the secret as a spot on the Y-axis and then choose a random point in space. Now, we have a line through the Y-axis and the random point which enables us to generate as many secret shares as we want. In this case we need only \(2 \) people to recover the secret.
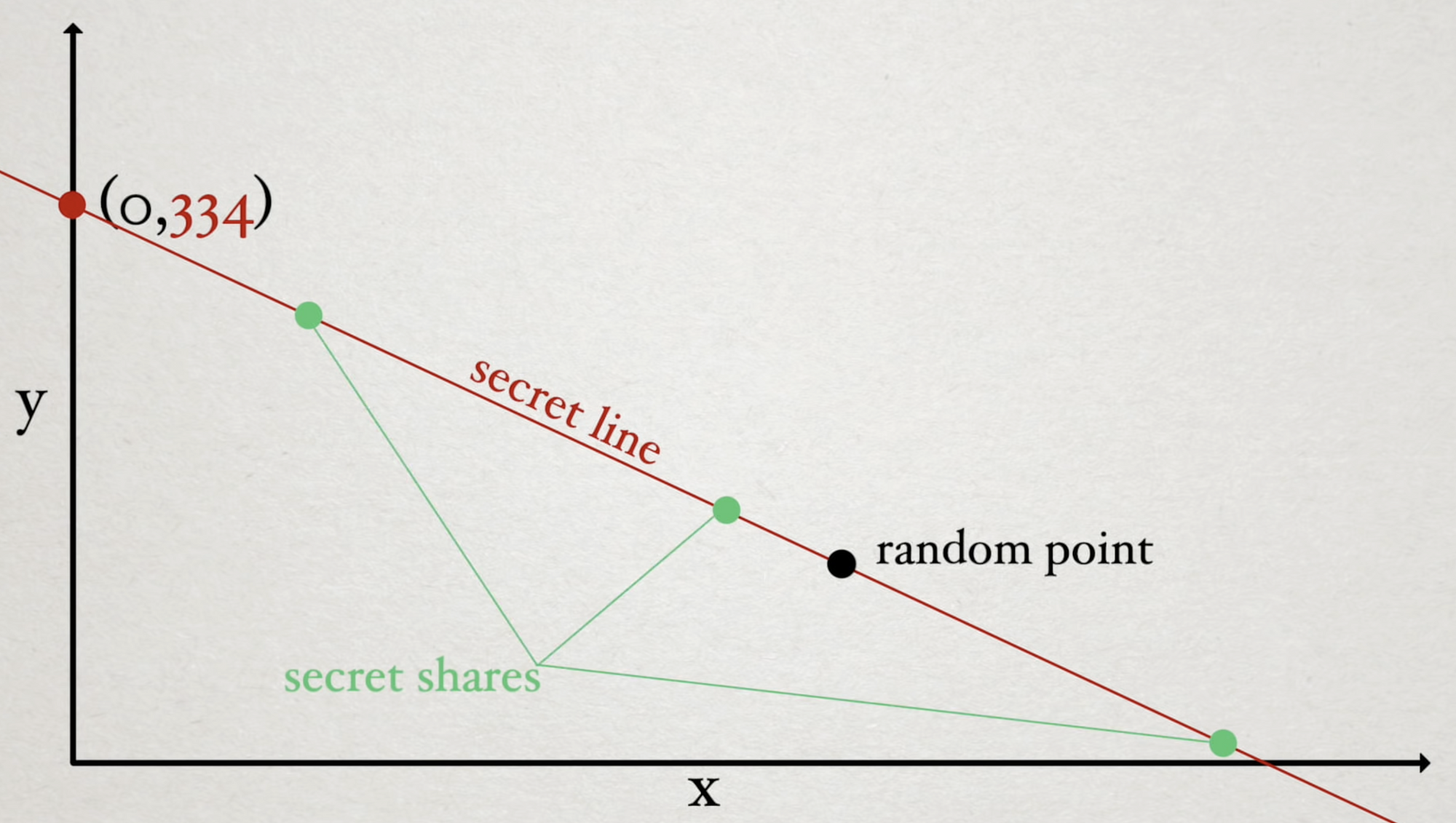
To increase the number of people needed to recover a secret, we need only increase the degree of the polynomial turning the line into a curve. In the case of three people (\( 3n \) scheme), in order to solve for a given parameter, we are going to need 3 points along the curve to determine the Y-intercept.
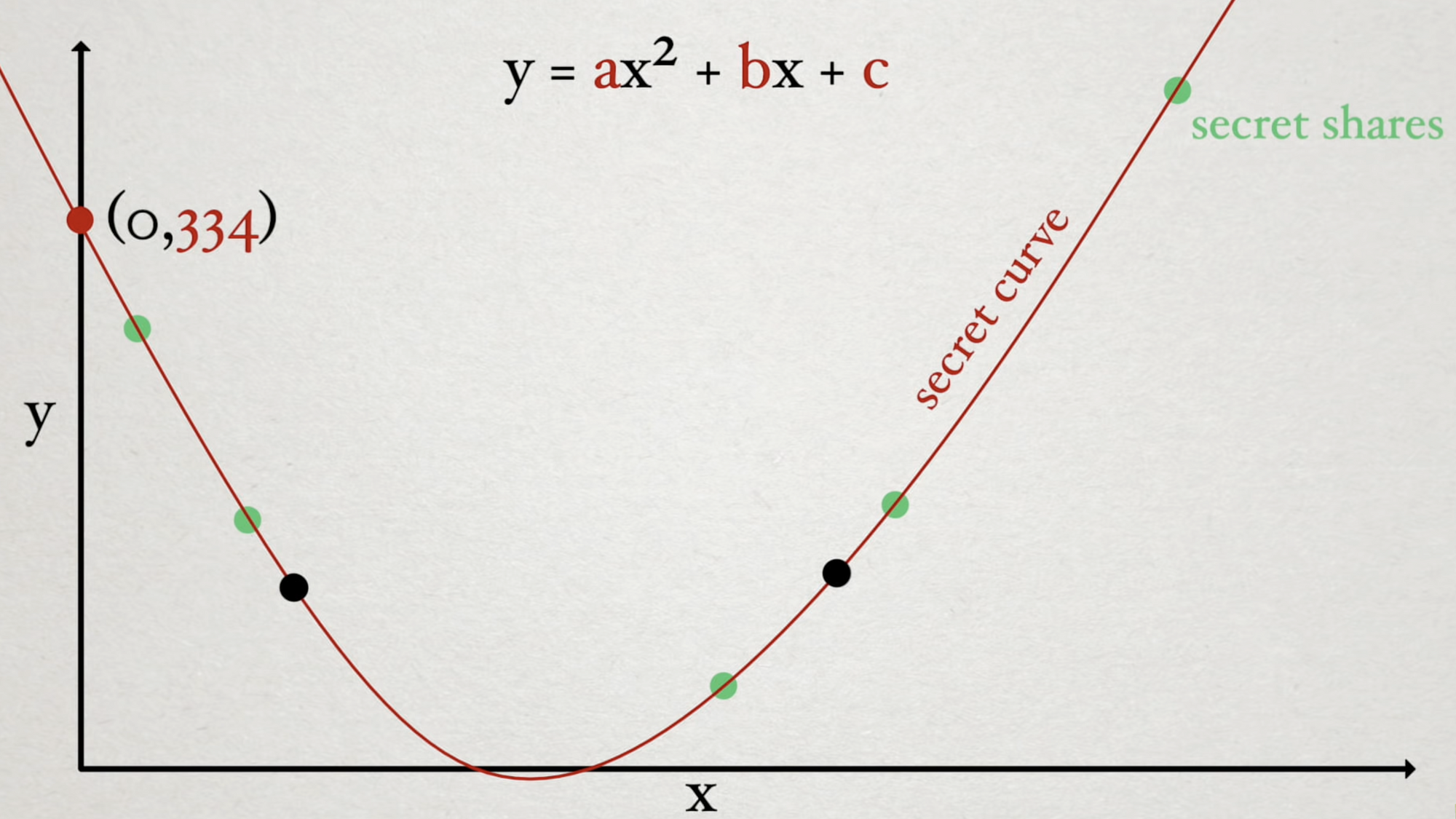
In the case of a \( 4n \) scheme, we would use a cubic curve where we need four points to define and recover the secret in the same way.
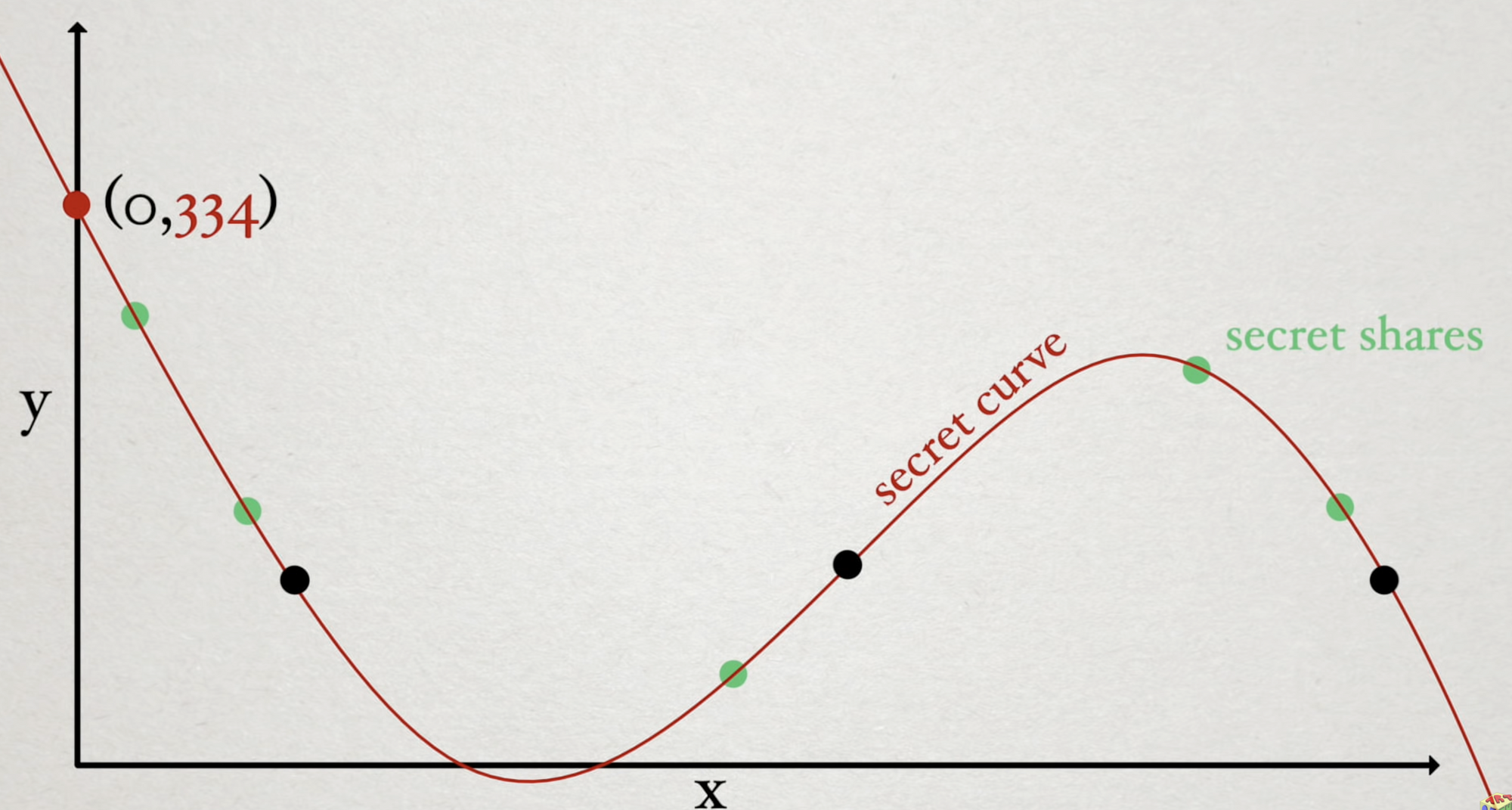
Shamir points out that this solution can be generalized using a polynomial of degree (\ k-1 \). For example, if you wanted to have a \( 10n \) scheme, you'd need a \( 9 \) degree polynomial.
Finally, given this scheme, can we do the polynomial interpolation quickly? Shamir points to The Design and Analysis of Computer Algorithms for more information on that. More recently, work has been done to reduce the polynomial division required yielding algorithms that rather than being \( \mathcal{O}(n\, log^2\, n) \) are \( \mathcal{O}(log^2\, n) \).
